原帖由 伊丽莎白女王 于 2006-12-18 13:30 发表
一般 几何 还是 解析集合啊?





原帖由 伊丽莎白女王 于 2006-12-18 13:30 发表
一般 几何 还是 解析集合啊?


原帖由 伊丽莎白女王 于 2006-12-18 15:15 发表
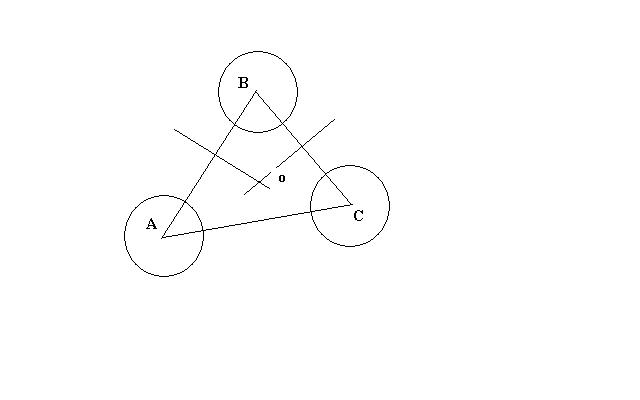
如果这 3 个圆 的圆心位置 在 1 条线上, 还有讨论的意义吗?

原帖由 seefilm 于 2006-12-18 15:13 发表
错误,上图中AC最高点连接上直线和B下方的交点,就比你那个最大角大。
原帖由 伊丽莎白女王 于 2006-12-18 15:29 发表


那感觉出这种题目没有什么意思啊!!
原帖由 伊丽莎白女王 于 2006-12-18 15:15 发表
如果这 3 个圆 的圆心位置 在 1 条线上, 还有讨论的意义吗?

原帖由 Klein_Yu 于 2006-12-18 15:21 发表
首先,我说这道题有点挑战性,是因为它没有说清楚,看角最大最小,是什么范围内!
这个角可以是钝角、也可以是锐角。
所以,我所给出的解法,如果你算角abc的钝角的话,则完全正确。
如果三个圆的圆 ...
 证明过程万一蒙上了说不定还能捞点儿分儿。
证明过程万一蒙上了说不定还能捞点儿分儿。 。。。明显若想找大角的话应该往下面两个园的左右外侧找呀,你敢说从里侧弄了个角就说大小通吃
。。。明显若想找大角的话应该往下面两个园的左右外侧找呀,你敢说从里侧弄了个角就说大小通吃 即便是找最小角的问题,显然从你那个顶点往下面两个园内侧引切线也比你那个小呀
即便是找最小角的问题,显然从你那个顶点往下面两个园内侧引切线也比你那个小呀 貌似你随便发现了两个角然后就主张是最大或者最小的说
貌似你随便发现了两个角然后就主张是最大或者最小的说
原帖由 chinesesongs 于 2006-12-18 17:32 发表
这道题关键是证明结果吧,光给答案非应试手段呀证明过程万一蒙上了说不定还能捞点儿分儿。
。。。更何况答案如果不对,那一分儿也得不了了 。。。就比如你这个。。。明显若想找 ...
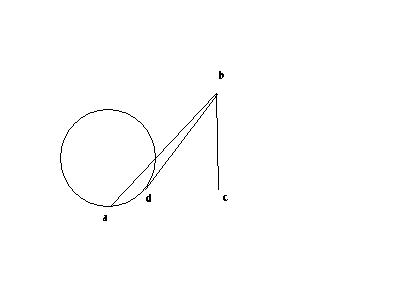
原帖由 chinesesongs 于 2006-12-18 18:04 发表
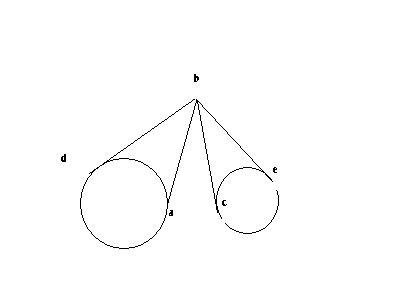
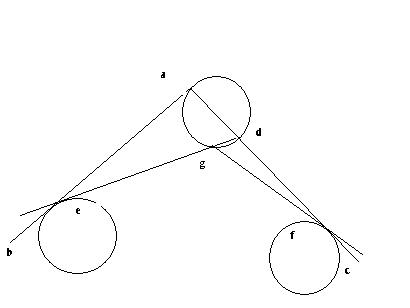
找大角的话,你倒是说说下面abc和dbe哪个更大:naughty:
原帖由 chinesesongs 于 2006-12-18 18:04 发表
找大角的话,你倒是说说下面abc和dbe哪个更大:naughty:
原帖由 toothy 于 2006-12-18 19:12 发表
不用讨论了。我只提示大家一句话:
大角对大边
设法找到可能的最长边,然后找对应角。
所以说是中学问题。
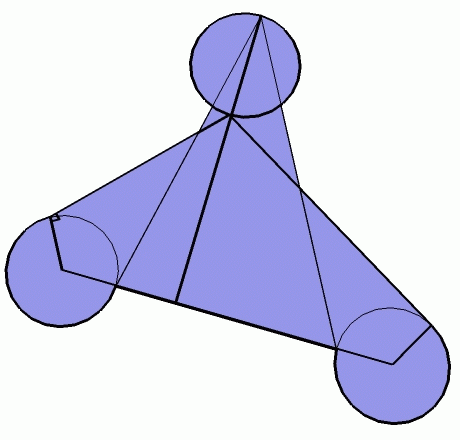

 原来答案这么简单呀。。。
原来答案这么简单呀。。。
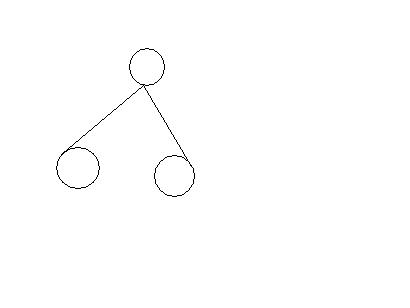
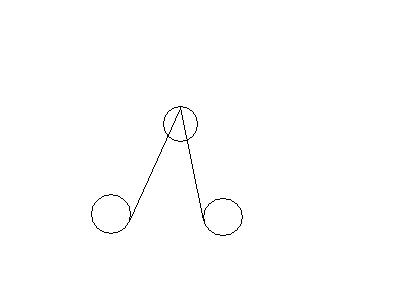
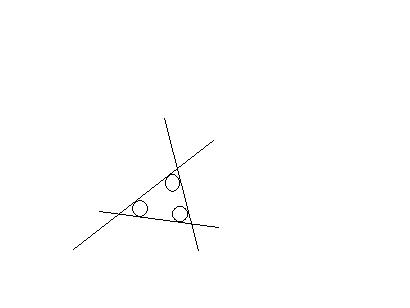


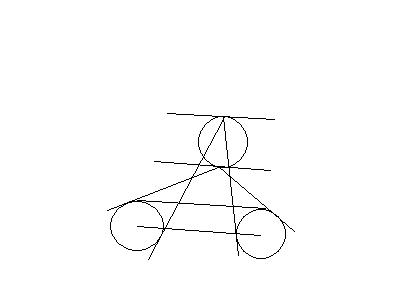
 。。。
。。。
原帖由 Klein_Yu 于 2006-12-18 19:37 发表
不好意思,我承认我之前的解法有点问题。不过,麻烦你看看我之前修改的解法。
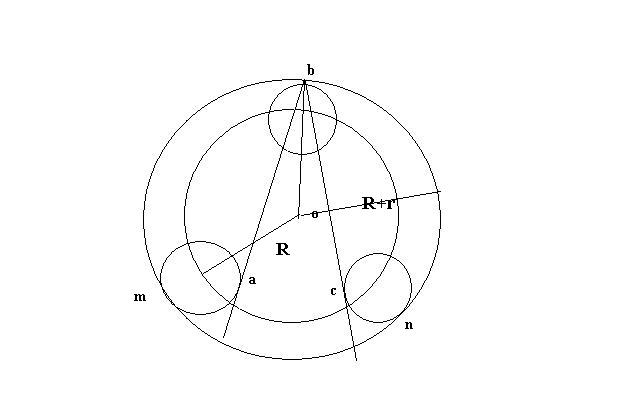
我的思路主要是要先确定下圆B上的b点。因为,三个圆是等圆的关系,所以先通过三个圆心找到一个大圆的圆心,作大圆。然后交 ...


原帖由 chinesesongs 于 2006-12-19 14:23 发表
这么客气
说说你的证明
原帖由 chinesesongs 于 2006-12-19 13:48 发表
然后的问题是顶点该选在那个圆的什么位置。首先在另外两个圆对着顶点所在圆的那一侧做切线(这个切线在等圆的条件下其实就是圆心连线的平行线)。然后在顶点所在圆的外侧和内侧分别做下面两个圆外切线的平行线, ...






原帖由 Klein_Yu 于 2006-12-19 17:39 发表
你先看看之前,我给出的解法。主要思路是要找出一个大圆,它经过三个圆圆心。
按照你画三角形的或者大角对大边的说法,只要找到圆心o,就可以找到了对应于最大角或者最小角的顶点b了,对应于o点的距离最大 ...

| 欢迎光临 人在德国 社区 (http://csuchen.de/bbs/) | Powered by Discuz! 7.2 |