原帖由 keynes06062006 于 2006-7-9 14:55 发表
猫是机器猫,只要有电就OK,老鼠也是的,淹不死

原帖由 chairmanqin 于 2006-7-9 11:19 发表
不用这么麻烦吧。。。
原帖由 驴子 于 2006-7-9 12:49 发表
啥到逃掉啊,上了岸还是可以继续追得
V对4V,上了岸总会被追上的吧
原帖由 驴子 于 2006-7-9 12:49 发表
啥到逃掉啊,上了岸还是可以继续追得
V对4V,上了岸总会被追上的吧
原帖由 驴子 于 2006-7-9 12:55 发表
印象中老鼠是在水池中间
走的路线是条弧线,老鼠每一时刻逃跑的方向是它和猫当前位置连线的反方向
原帖由 jiejiedog 于 2006-7-9 12:56 发表
用到极坐标。
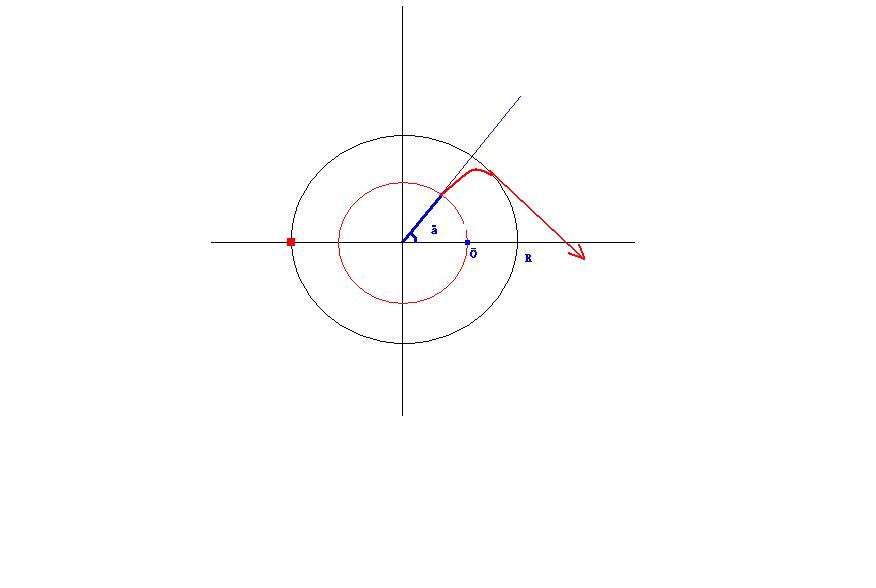
我的想法是,t=0时,老鼠距离圆心距离为X,与半径夹角为SIGMA,背对猫。
接下去就是计算,老鼠速度在半径方向上的分量的积分等于半径+X的时候,猫的速度(只有切线方向的分量)的积分到达老鼠对着 ...
原帖由 zizidodoII 于 2006-7-9 12:59 发表
跟我想法一样 但是不能假设在圆心 否则没意义了 :D
原帖由 驴子 于 2006-7-9 13:01 发表
能不能在圆心用matlab模拟一下就可以了
让狗狗做一个,然后帖上来lol.gif
原帖由 驴子 于 2006-7-9 13:01 发表
能不能在圆心用matlab模拟一下就可以了
让狗狗做一个,然后帖上来lol.gif
原帖由 bluestem 于 2006-7-9 13:16 发表
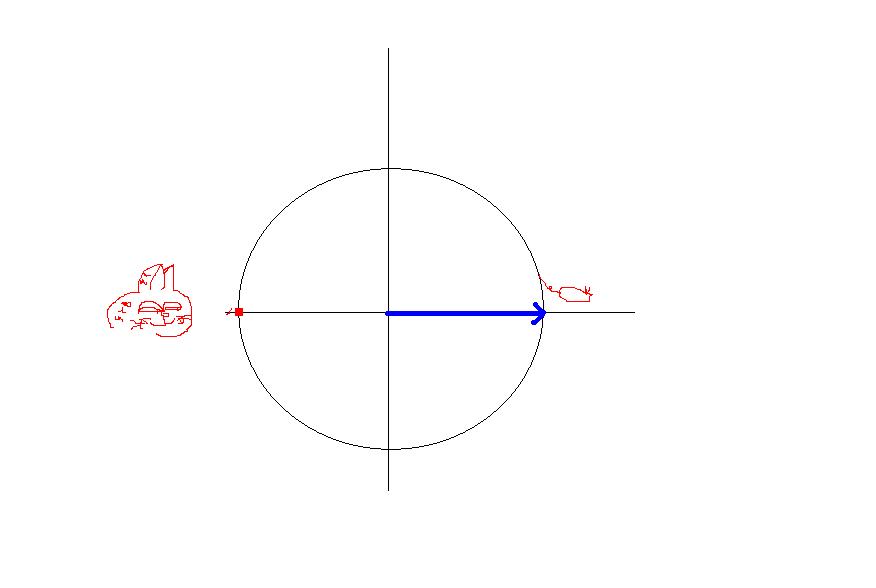
为什么方向是死的,老鼠可以边往岸边游,边改变方向,弧线运动。
原帖由 zizidodoII 于 2006-7-9 13:22 发表
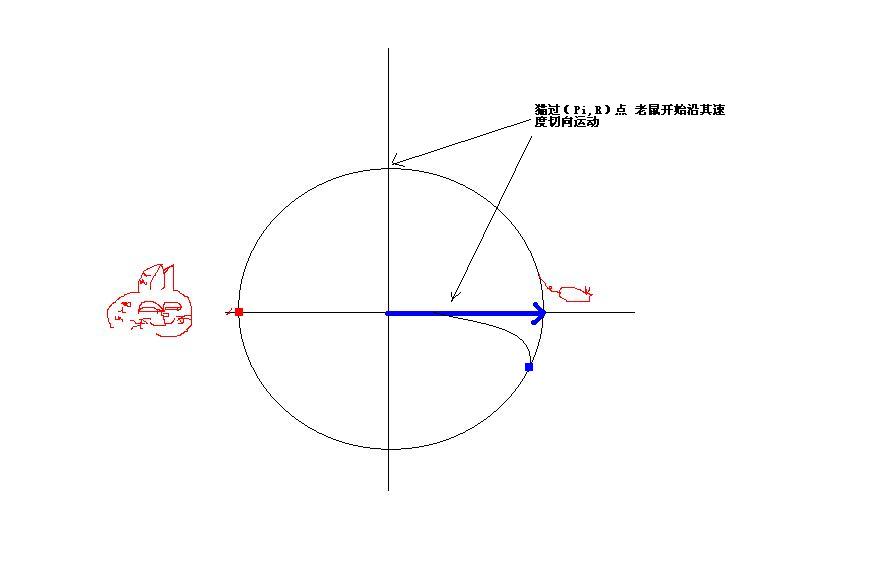
对哦 那 jiejiedog的算法估计要换一下了 我考虑只有当猫过了 1/4圆周的时候 才开始切线方向运动 靠 那不在圆心的就更复杂了…… 晕了
原帖由 bluestem 于 2006-7-9 13:22 发表
初始条件可以定在圆心,如果老鼠够聪明的话,当然是游到中间最安全的地方,然后考虑最安全的路线逃出去,不然你给它算出来安全路线,它一样笨到往猫的方向跑。
如果初始条件是老鼠和猫在直径的两头呢lol.gif
原帖由 jiejiedog 于 2006-7-9 13:25 发表
我的不用换,我就是这么考虑的呀,所以sigma在不停的变。
楼上有道理,可以考虑从圆心开始,简化问题
原帖由 zizidodoII 于 2006-7-9 13:29 发表
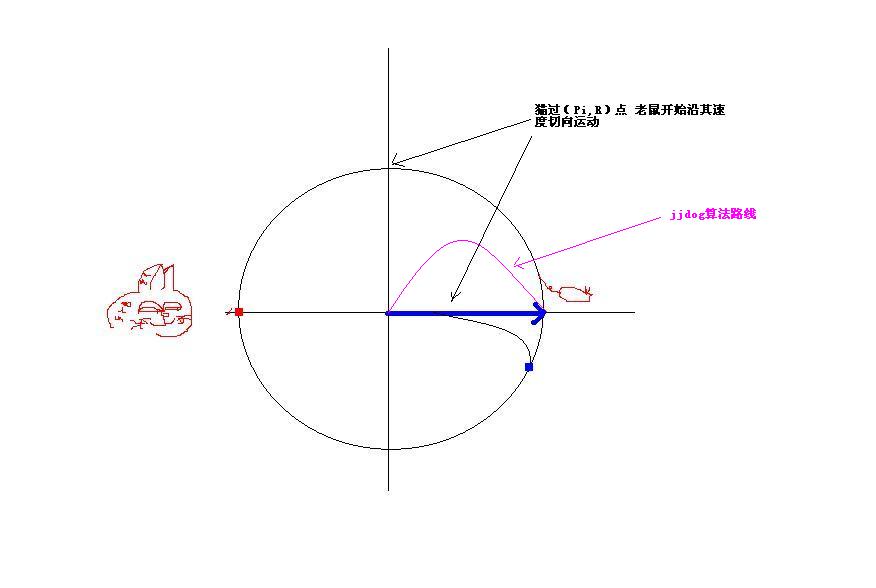
"我的想法是,t=0时,老鼠距离圆心距离为X,与半径夹角为SIGMA,背对猫。
接下去就是计算,老鼠速度在半径方向上的分量的积分等于半径+X的时候,猫的速度(只有切线方向的分量)的积分到达老鼠对着的 ...
原帖由 jiejiedog 于 2006-7-9 13:43 发表
你的画图技术真强!用鼠标画的么?
原帖由 toothy 于 2006-7-9 14:46 发表
题目本身没有定义清楚,猫(鼠)怎样决定向左或向右追(游)
所以题目还缺乏一些条件,如果先假设:
1。猫和鼠都足够聪明,以致于他们能分别根据任意一时刻两者的位置,计算出下一步该向那个方向捕捉(逃生) ...
原帖由 toothy 于 2006-7-9 14:46 发表
题目本身没有定义清楚,猫(鼠)怎样决定向左或向右追(游)
所以题目还缺乏一些条件,如果先假设:
1。猫和鼠都足够聪明,以致于他们能分别根据任意一时刻两者的位置,计算出下一步该向那个方向捕捉(逃生)。。
2。老鼠可以在无穷的时间内在水池中游动。
原帖由 jiejiedog 于 2006-7-9 14:46 发表
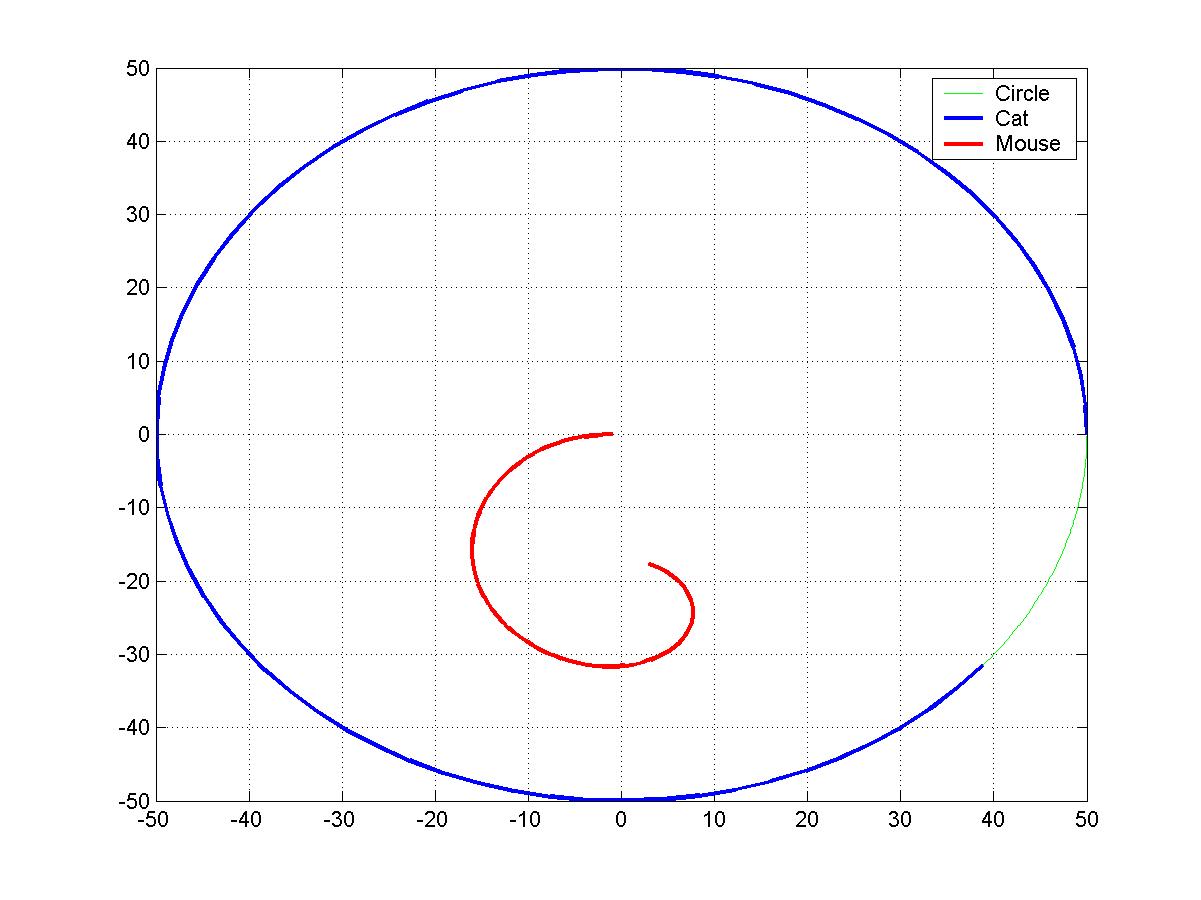
我先用差分方程算了一下,解析法还没做。
从图上看,老鼠怎么也逃不了了。
我换了好几个初始条件,结果都是一样的。
原帖由 zizidodoII 于 2006-7-9 14:52 发表
初始条件都是默认在圆心? 如果不在圆心还是能逃的吧 另外别上来就跟猫的切线走啊 现象径向反方向走 知道猫的切线和径向反方向平行才开始切线吧 估计有难度 jjd 靠你了
原帖由 sailorman 于 2006-7-9 14:53 发表
别算了,兜圈圈,最后猫累死了,老鼠淹死了

原帖由 zizidodoII 于 2006-7-9 14:52 发表
初始条件都是默认在圆心? 如果不在圆心还是能逃的吧 另外别上来就跟猫的切线走啊 现象径向反方向走 知道猫的切线和径向反方向平行才开始切线吧 估计有难度 jjd 靠你了
原帖由 keynes06062006 于 2006-7-9 14:55 发表
猫是机器猫,只要有电就OK,老鼠也是的,淹不死
原帖由 jiejiedog 于 2006-7-9 15:00 发表
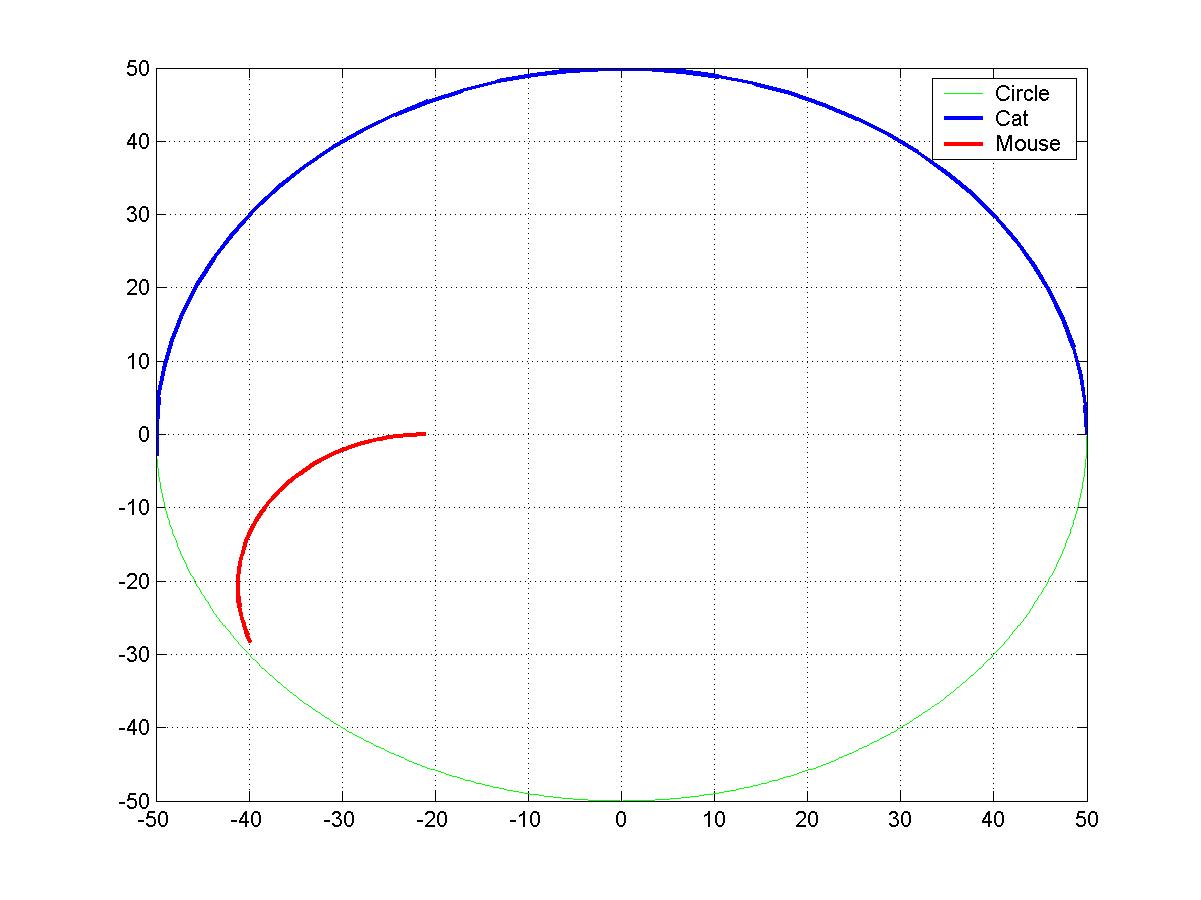
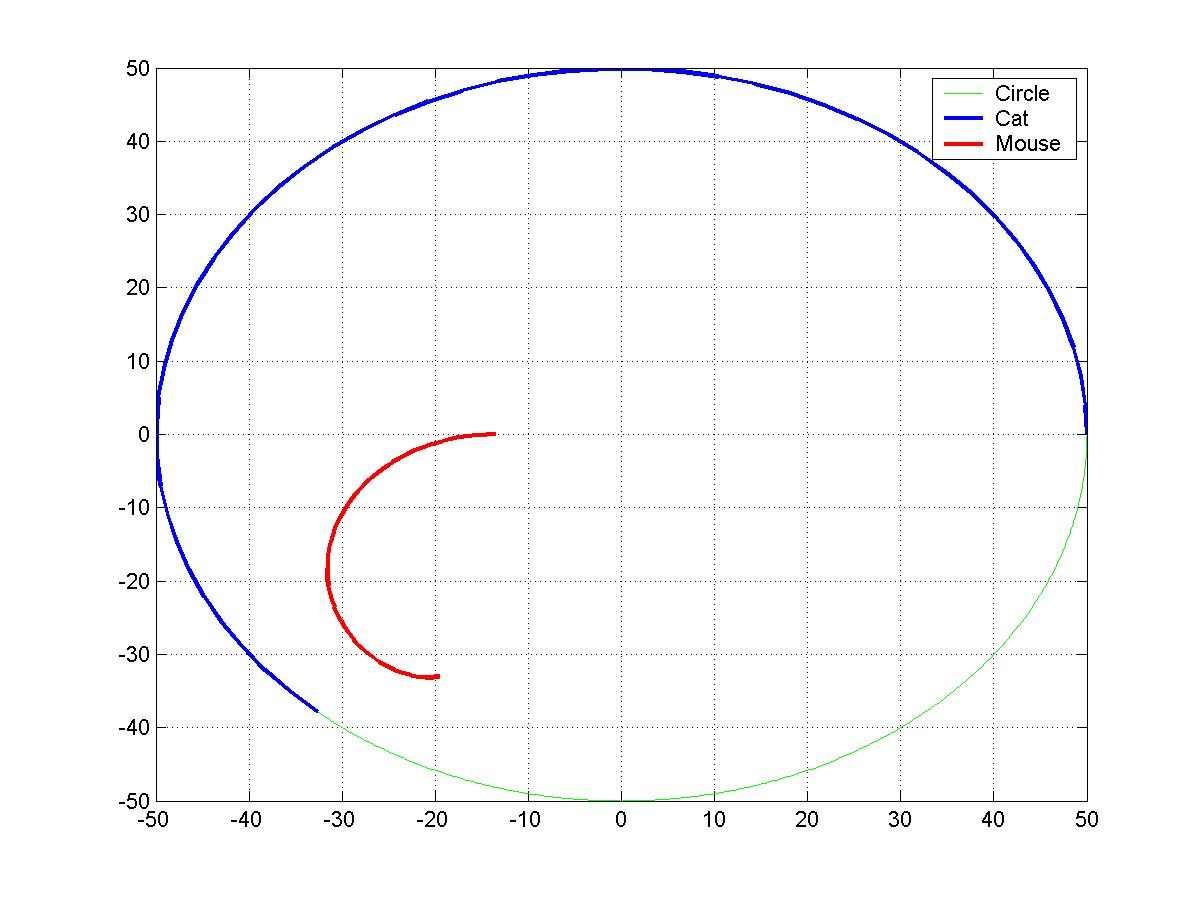
从头到尾我都没有考虑过切线的问题啊。我一直设定老鼠的屁股对着猫的位置。思路如下,也许有错误,仅供参考。
clear
clc
close all
R=50;
V_mouse=10;
V_cat=4*V_mouse;
Delta_t=0.1;
t=0:Delt ...
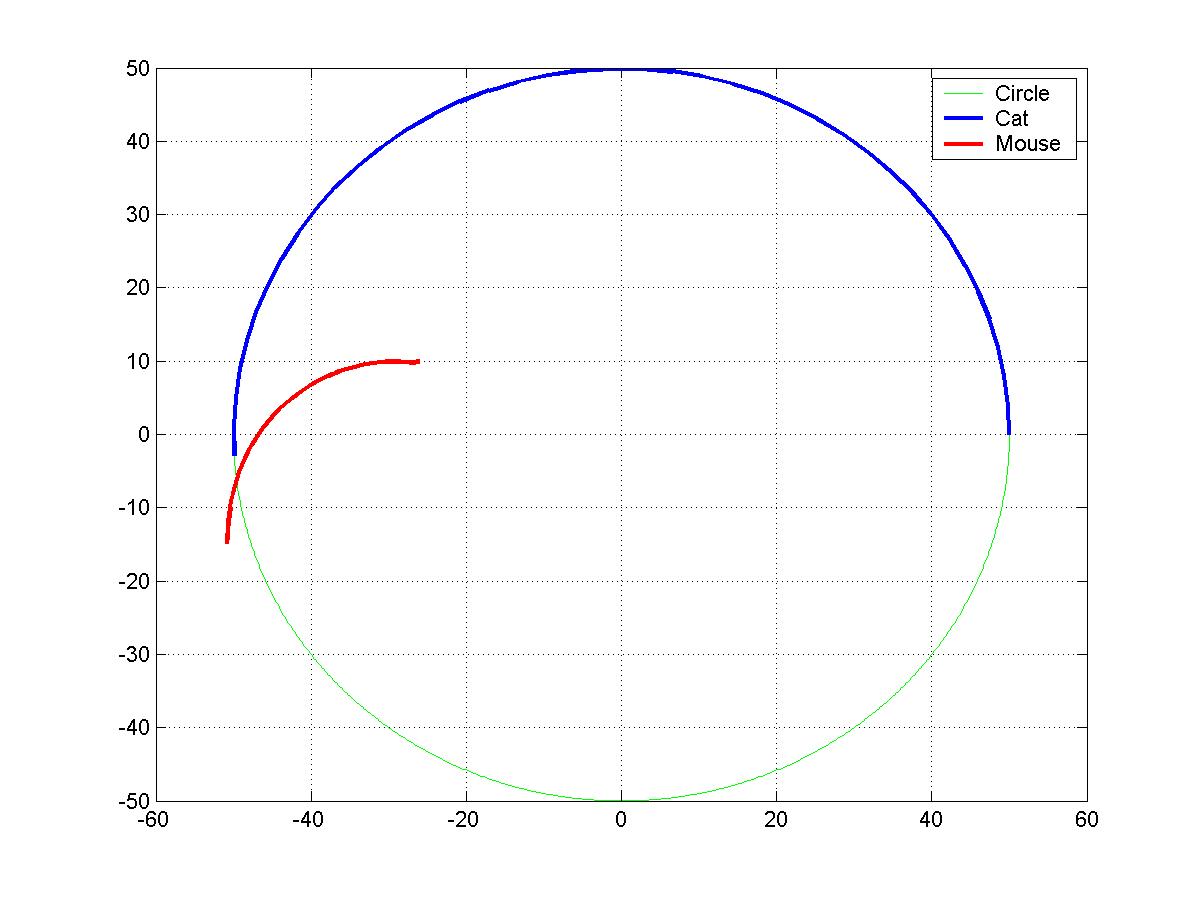
原帖由 jiejiedog 于 2006-7-9 15:08 发表
如果猫和老鼠连线初始状态不在直径上,情况可能如下
满足某些情况下,老鼠可以逃出去。

原帖由 sailorman 于 2006-7-9 15:12 发表
我觉得假设应该是老鼠距离猫最远的地方开始,也就是水池的中央,圆心。这样才可能只有一个答案。
不然假设就多了点。
原帖由 zizidodoII 于 2006-7-9 15:16 发表
一个答案是存在通话和初等数学中
jjd这么高人 不做一个答案的题 哈哈哈
原帖由 zizidodoII 于 2006-7-9 15:16 发表
一个答案是存在通话和初等数学中
jjd这么高人 不做一个答案的题 哈哈哈
原帖由 zizidodoII 于 2006-7-9 15:16 发表
一个答案是存在通话和初等数学中
jjd这么高人 不做一个答案的题 哈哈哈
原帖由 jiejiedog 于 2006-7-9 15:19 发表
这个题目是有确定答案的,满足某些条件的时候能够逃出,就是老鼠初始情况偏离圆心的位置(x,y)都有影响。最后应该通过解析法做,刚才只是直观的迭代出来看看。
原帖由 neig_xp 于 2006-7-9 15:26 发表
我觉得这个题要看猫是怎么想得了。如果猫只朝一个方向追(比如顺时针),那么老鼠肯定跑掉了,如果猫自动判断优弧劣弧然后从劣弧方向追,那么老鼠只用走s形就能跑掉,要是猫和老鼠都比我聪明,那我就不知道他们俩 ...
原帖由 toothy 于 2006-7-9 15:36 发表
想法1:
如果能有这样一个时刻,此时,老鼠位于圆内一点 P,P 到圆弧的最近线段为 PA,长度|PA|,而猫位于圆弧上一点Q,圆弧QA弧长为|QA|,并且:|QA|大于4倍的|PA|,那么,老鼠就1定能逃脱。

原帖由 jiejiedog 于 2006-7-9 16:43 发表
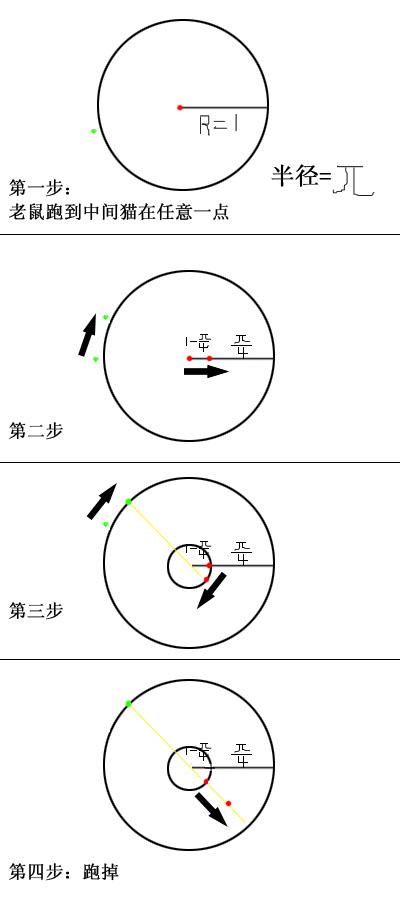
明白意思了:
如果老鼠使用策略,最多也就是在半径为R/4的圆周上,出了这个圈猫的角速度就超过老鼠。
那么假设现在老鼠站在距离猫5R/4的直径上(通过和猫拉角速度总可以做到这点),反方向跑。有两种可能
一 ...
原帖由 keynes06062006 于 2006-7-9 17:15 发表
答案是老鼠能跑掉的
原帖由 jiejiedog 于 2006-7-9 17:17 发表
但是他耍诈了,只有人才那么聪明tired.gif
原帖由 jiejiedog 于 2006-7-9 17:13 发表
猫跑直线跑到对面那个点需要的时间是:pi*R/(4*V)
而老鼠需要的时间是:3×R/(4*V)
pi*R/(4*V)>3×R/(4*V)
也就是说猫要跑到对面需要的时间大于老鼠到达岸边的时间啊……
| 欢迎光临 人在德国 社区 (http://csuchen.de/bbs/) | Powered by Discuz! 7.2 |